-
Rappelez la définition d'une population stationnaire.
Montrez en particulier que si les individus de la population ne sont
pas classés selon leur âge mais selon le temps qui leur reste à
vivre, la pyramide obtenue, appelée pyramide des années à vivre, est
identique à la pyramide des âges.
Voir le cours.
-
On s'intéresse désormais à l'épidémie de sida dans un pays occidental
avant l'année 1985. Avant cette date, la croissance de l'épidémie
correspondait à un temps de doublement annuel des nouveaux cas de
sida. Prouvez que le taux de croissance infinitésimale était alors de
69,3 % par an.
Le taux de doublement est relié au taux de croissance par la
relation :
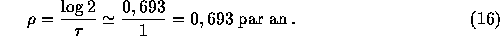
-
On peut supposer que la population des infectés était
une population stable. La variable importante n'est donc plus l'âge
mais le temps depuis l'infection. Les entrées correspondent aux
nouvelles infections, les sorties à la déclaration du sida.
On suppose que la force 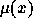 de déclaration du sida (l'équivalent
de la force de mortalité) est une fonction connue. Donner l'expression
de la fonction de survie à l'état asymptomatique ainsi que l'espérance
de vie d'un nouvel infecté en fonction de
de déclaration du sida (l'équivalent
de la force de mortalité) est une fonction connue. Donner l'expression
de la fonction de survie à l'état asymptomatique ainsi que l'espérance
de vie d'un nouvel infecté en fonction de 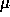 .
.
La probabilité de survie jusqu'à l'âge x est :
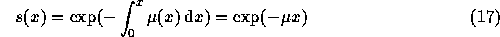
L'espérance de vie est donc :
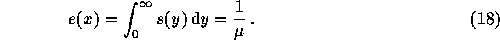
-
Si on suppose pour simplifier que la force de déclaration de la
maladie est indépendante du temps depuis l'infection,
dessiner la fonction de survie à l'état asymptomatique sachant que
l'espérance de vie asymptomatique est d'environ 10 années.
Il s'agit d'une simple exponentielle.
-
La situation avant 1985 est fortement épidémique et est supposée
stable (au sens démographique du terme). Ecrire l'équation fondamentale
d'une population stable (ou malthusienne) reliant la composition
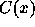 par
durée d'infection x à la force
par
durée d'infection x à la force 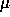 et au taux de croissance
et au taux de croissance 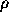 .
.
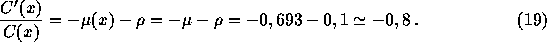
-
Dessiner la pyramide des infectés suivant le temps depuis l'infection.
Il s'agit d'une exponentielle nettement plus décroissante puisque le
taux de décroissance est 69,3+10 % par an.
-
On s'intéresse désormais plutôt au classement à une date t des
infectés, non pas suivant le temps, x, depuis l'infection
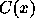 mais le temps y restant avant la déclaration du sida. Donner
l'expression de la composition
mais le temps y restant avant la déclaration du sida. Donner
l'expression de la composition 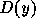 .
Si à la date t la composition par âge est
.
Si à la date t la composition par âge est 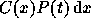 individus âgés entre les âges x et
individus âgés entre les âges x et 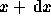 , à la date t+y une
proportion
, à la date t+y une
proportion 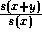 atteindra l'âge x+y. Parmi ces
derniers une proportion
atteindra l'âge x+y. Parmi ces
derniers une proportion 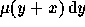 décèdera entre les temps
t+y et
décèdera entre les temps
t+y et 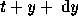 , c'est à dire sera à y années de la mort.
, c'est à dire sera à y années de la mort.
Si on cumule sur tous les âges x, on obtient :
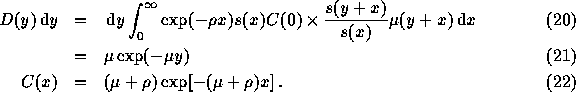
On retrouve en effet dans le cas d'une force indépendante du temps
passé dans l'état, que la durée 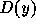 est indépendante de la
croissance et égale à la distribution des décès
du cas stationnaire.
est indépendante de la
croissance et égale à la distribution des décès
du cas stationnaire.
-
Tracer sur une même courbe les deux pyramides qui ont donc un volume
(taille) identique. Calculer à une date t l'ancienneté moyenne
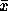 de la population des infectés, et la durée de survie moyenne
à l'état asymptomatique
de la population des infectés, et la durée de survie moyenne
à l'état asymptomatique 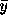 .
.
L'ancienneté moyenne dans la maladie est :
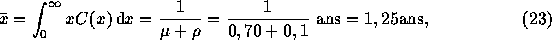
et la durée de survie asymptomatique moyenne des séropositifs est
donc 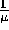 = 10 ans.
= 10 ans.
-
Donner la distribution suivant l'ancienneté de la maladie des cas de
sida survenus entre les instants t et
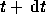 . Quelle est
l'ancienneté moyenne des cas de sida ? Pourquoi est-elle si courte
comparée aux 10 ans de survie asymptomatique moyenne ? Pourquoi
pensait-on à cette époque, en observant les cas dans les hôpitaux que
la durée d'incubation était très courte ?
. Quelle est
l'ancienneté moyenne des cas de sida ? Pourquoi est-elle si courte
comparée aux 10 ans de survie asymptomatique moyenne ? Pourquoi
pensait-on à cette époque, en observant les cas dans les hôpitaux que
la durée d'incubation était très courte ?
La distribution des nouveaux cas de sida classés suivant la durée
depuis l'infection est :
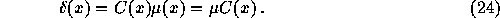
Dans les hôpitaux, les nouveaux cas de sida avait donc une
ancienneté moyenne égale à 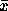 =1/70=1,4 an soit très courte en
comparaison de la durée moyenne d'incubation. Dans la population des
séropositifs, il y avait beaucoup plus de nouveaux infectés que
d'anciens en raison de la croissance. Ainsi même si en moyenne les
nouveaux infectés déclareront un sida 10 ans plus tard, certains
déclarent par manque de chance un sida très tôt, ce sont ceux là
qu'on trouve dans les hôpitaux, et is sont en majorité en raison de
la forte croissance. Les médecins, c'est à dire les personnes
les plus concernées par cette nouvelle maladie puisque ce sont eux
qui ont découvert les premiers cas, ont longtemps pensé qu'il
s'agissait d'une maladie très ``mortelle'' c'est à dire d'une maladie
dont la durée d'incubation était très courte puisqu'effectivement
les cas qu'ils traitaient avaient été infectés très récemment (sans
connaitre la date exacte de l'infection, certains malades
connaissaient et ont même publié leur date vraisemblable d'infection).
=1/70=1,4 an soit très courte en
comparaison de la durée moyenne d'incubation. Dans la population des
séropositifs, il y avait beaucoup plus de nouveaux infectés que
d'anciens en raison de la croissance. Ainsi même si en moyenne les
nouveaux infectés déclareront un sida 10 ans plus tard, certains
déclarent par manque de chance un sida très tôt, ce sont ceux là
qu'on trouve dans les hôpitaux, et is sont en majorité en raison de
la forte croissance. Les médecins, c'est à dire les personnes
les plus concernées par cette nouvelle maladie puisque ce sont eux
qui ont découvert les premiers cas, ont longtemps pensé qu'il
s'agissait d'une maladie très ``mortelle'' c'est à dire d'une maladie
dont la durée d'incubation était très courte puisqu'effectivement
les cas qu'ils traitaient avaient été infectés très récemment (sans
connaitre la date exacte de l'infection, certains malades
connaissaient et ont même publié leur date vraisemblable d'infection).
-
Si on supose qu'après 1985, il n'y a plus de nouvelles infections du
tout. Tracer les deux pyramides en 1995. Discuter.
La pyramide suivant la durée d'infection a un creux, par contre la
pyramide suivant la durée de survie est toujours une exponentielle.
![]()
![]() de déclaration du sida (l'équivalent
de la force de mortalité) est une fonction connue. Donner l'expression
de la fonction de survie à l'état asymptomatique ainsi que l'espérance
de vie d'un nouvel infecté en fonction de
de déclaration du sida (l'équivalent
de la force de mortalité) est une fonction connue. Donner l'expression
de la fonction de survie à l'état asymptomatique ainsi que l'espérance
de vie d'un nouvel infecté en fonction de ![]() .
.![]()
![]()
![]()
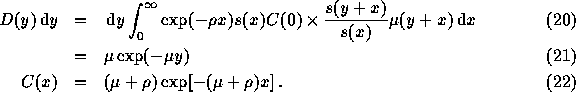
![]() est indépendante de la
croissance et égale à la distribution des décès
du cas stationnaire.
est indépendante de la
croissance et égale à la distribution des décès
du cas stationnaire.
![]()
![]() = 10 ans.
= 10 ans.
![]()
![]() =1/70=1,4 an soit très courte en
comparaison de la durée moyenne d'incubation. Dans la population des
séropositifs, il y avait beaucoup plus de nouveaux infectés que
d'anciens en raison de la croissance. Ainsi même si en moyenne les
nouveaux infectés déclareront un sida 10 ans plus tard, certains
déclarent par manque de chance un sida très tôt, ce sont ceux là
qu'on trouve dans les hôpitaux, et is sont en majorité en raison de
la forte croissance. Les médecins, c'est à dire les personnes
les plus concernées par cette nouvelle maladie puisque ce sont eux
qui ont découvert les premiers cas, ont longtemps pensé qu'il
s'agissait d'une maladie très ``mortelle'' c'est à dire d'une maladie
dont la durée d'incubation était très courte puisqu'effectivement
les cas qu'ils traitaient avaient été infectés très récemment (sans
connaitre la date exacte de l'infection, certains malades
connaissaient et ont même publié leur date vraisemblable d'infection).
=1/70=1,4 an soit très courte en
comparaison de la durée moyenne d'incubation. Dans la population des
séropositifs, il y avait beaucoup plus de nouveaux infectés que
d'anciens en raison de la croissance. Ainsi même si en moyenne les
nouveaux infectés déclareront un sida 10 ans plus tard, certains
déclarent par manque de chance un sida très tôt, ce sont ceux là
qu'on trouve dans les hôpitaux, et is sont en majorité en raison de
la forte croissance. Les médecins, c'est à dire les personnes
les plus concernées par cette nouvelle maladie puisque ce sont eux
qui ont découvert les premiers cas, ont longtemps pensé qu'il
s'agissait d'une maladie très ``mortelle'' c'est à dire d'une maladie
dont la durée d'incubation était très courte puisqu'effectivement
les cas qu'ils traitaient avaient été infectés très récemment (sans
connaitre la date exacte de l'infection, certains malades
connaissaient et ont même publié leur date vraisemblable d'infection).