Espérance de vie
Il s'agit de
l'espérance de vie à la naissance de la population avant l'épidémie de
sida. Elle est prise égale à 50 ans dans l'ouvrage ce qui correspond à
la réalité africaine du début des années 90. L'espérance de vie est
l'espérance mathématique de la durée de vie aléatoire d'une cohorte
fictive de nouveau-nés nés vivants et soumis jusqu'à l'extinction de
la cohorte aux risques de décéder à chaque âge. Ces risques de
décéder sont estimés en rapportant des décès observés entre deux âges
et deux dates à l'effectif de la population soumise au risque de décès
entre ces deux âges et durant ces deux dates. On obtient ainsi des
taux de mortalité par âge pour la période. Leur dimension est
l'inverse d'un temps comme une incidence ou une fréquence et s'exprime
le plus souvent en démographie en par an.
Un indice couramment présenté et qui peut généralement se déduire du
taux de mortalité par âge est la probabilité de décéder entre deux
âges exacts (quotient de mortalité en français), comprise entre 0 et
1. On trouve des exemples de quotients de mortalité avant l'épidémie
et après l'épidémie sur la figure
25 de la page 159.
La décroissance de la cohorte fictive est retracée dans la fonction de
survie de la figure
26. L'espérance de vie à la naissance est également l'aire située
sous la fonction de survie.
Si vous entrez une valeur de 20 ou 25 ans, vous obtenez la situation
d'avant la transition démographique c'est à dire des conditions de
mortalité qui ont vraisemblablement prévalu depuis que l'homme existe
jusqu'à la fin du XVIIIe siècle en Europe et du début du siècle en
Afrique.
Si vous entrez une valeur de 75 ans, vous serez proche
de la situation contemporaine des pays développés.
Par défaut la table de mortalité choisie dans ce modèle est une table-type appartenant au modèle ouest des tables
dites de Coale et Demeny. Ces différentes autres régions (est, nord,
sud) permettent pour un même niveau d'espérance de vie d'obtenir
différents profils par âge (il s'agit d'un raffinement pour
démographes). Ici, on suppose arbitrairement que les hommes ont une
espérance de vie inférieure de deux années à celle des
femmes. L'espérance de vie entrée est l'espérance de vie pour les deux
sexes.
Les tables types originales fournissent des taux de mortalité par âge
quinquennale, or pour simuler l'épidémie de sida il est nécessaire
d'obtenir des données par âge simple. Ainsi on a effectué un lissage
de la fonction de survie pour obtenir une table par âge
simple. Néanmoins la procédure utilisée, à savoir un lissage par
quasi-spline de Hermite n'est pas optimale et certaines vagues
indésirables sont observables pour les quotients les plus faibles sur
un graphique semi-logarithmique. Ces vagues n'ont aucune influence sur
les résultats de simulation.
Durant l'épidémie, la mortalité adulte va augmenter car ce sont les
adultes sexuellement actifs qui sont les plus touchés par
l'épidémie. La transmission dépend de nombreux facteurs expliqués dans
l'ouvrage. Ici, le niveau de la mortalité adulte est directement relié
à celui de la prévalence du VIH. La nouvelle
force de mortalité est égale à l'ancienne augmentée du produit de la
prévalence par l'inverse de la durée moyenne
d'incubation (on sous-entend ainsi que la déclaration du syndrome
est indépendante du temps depuis l'infection; ceci est inexact mais
suffisant pour la précision des résultats escomptés.
En raison de la transmission de la mère à l'enfant la mortalité infantile va également augmenter.
La fonction de survie durant l'épidémie sera doublement affectée:
durant les premières années de la vie et à l'âge adulte. L'espérance
de vie, qui est aussi l'aire située sous la courbe de survie,
diminuera.
La table de mortalité avant et durant l'épidémie peut être consultée
en cliquant sur les nouveaux libellés des figures.
Tables-types de mortalité: On a
remarqué que lorsque la mortalité d'un pays décroît au cours de sa
transition démographique, les quotients de mortalité par âge ne
décroissent pas d'un facteur rigoureusement identique à chaque âge mais
décroissent néanmoins à des rythmes spécifiques relativement
similaires. En particulier, les premiers progrès concernent
essentiellement la mortalité infantile et juvénile. Si l'on trace
l'ensemble des fonctions de survie d'un même pays depuis l'époque où
l'espérance de vie était de 25-30 ans jusqu'à aujourd'hui où elle peut
atteindre 80 ans, on décèle un réseau de tables qui traduit
la décroissance de la mortalité. En fait, en première approximation,
la mortalité de n'importe quel pays est supposée appartenir à ce
réseau à un seul paramètre, l'espérance de vie. En deuxième
approximation, on a remarqué que certains pays "du sud", comme
l'Espagne ou l'Italie, avaient pour un même niveau d'espérance de vie,
et quelque soit celui-ci, une mortalité infantile et juvenile plus
élevée que les autres pays (et réciproquement une mortalité adulte
plus basse). Pour être plus précis, on ajoute donc un second
paramètre. Certains auteurs, comme Coale et Demeny, ont créé des tables
dites régionales qui sont utilisées ici. Elles sont publiées par
groupe quinquennaux et pour certains niveaux seulement. Ici, on a
interpolé la fonction de survie pour obtenir des tables par âge simple
et propose des tables quelque soit le niveau d'espérance de vie. Les
résultats sont cohérents avec les résultats publiés :
Coale, Ansley and Demeny, Paul.- Regional Model Life Tables and
Stable Population, Princeton University Press, 1966, (édition
1983, Academic Press, 496 p.
Fécondité : Un taux annuel de fécondité par
âge est égal au nombre moyen d'enfants nés durant un an parmi les
femmes de cet âge. La courbe féminine par âge a une forme
caractéristique pour des raisons biologiques puisqu'elle croît à
partir de 15 ans puis redécroit pour être de nouveau nulle aux
environs de 50 ans, à l'âge de la ménopause. La courbe masculine est
surtout régit par la courbe féminine et le régime matrimonial. C'est
pourquoi nous distinguons ici deux régimes, européen ou africain.
Régime de
fécondité : Dans le régime européen récent la contraception,
largement utilisée, accentue la convexité de la courbe féminine après
30 ans. La fécondité des hommes aux âges élevés est faible car leurs
femmes (régime monogame) sont également du même âge et déjà
ménopausées. Dans certaines régions d'Afrique subsaharienne, l'écart
d'âge au premier mariage peut atteindre 10 ans, et les hommes
survivants aux âges élevés peuvent être mariés à des femmes
encore d'âge fécond, ce qui explique leur fécondité totale beaucoup
plus élevée que celles des femmes.
En cumulant les taux de fécondité sur tous les âges de la vie, on
obtient la descendance totale d'une cohorte de filles, en l'absence de
mortalité. Si, dans une enquête, on interroge les femmes de 50 ans sur
le nombre d'enfants qu'elles ont eu, on obtient le même chiffre si la
fécondité n'a pas changé. Pour les vieilles hommes des sociétés
polygames ce nombre total ne cesse d'augmenter en fonction de leur
âge. Dans l'exemple de la population des Peuls Bandé retenu ici, la
fécondité totale ou somme des naissances réduites est
supérieure à 12 enfants par homme et celle des femmes de l'ordre de
6,7 enfants par femme.
Descendance nette ou taux net de
reproduction: En Afrique en raison de la forte mortalité
infantile et juvénile, une cohorte initiale de futures mères ou de
futur pères perdra rapidement une partie de son effectif.
On peut ainsi voir sur la figure 27 et
le tableau de reproduction (accessible
qu'avec une visionneuse HTML 3.0) qu'en l'absence de sida les
générations africaines assuraient déjà leur remplacement (descendance
nette supérieure à 1 fille par fille) vers 23-24 ans. La descendance
finale nette s'établit autour de 2,43 filles par fille. Un taux de
reproduction inférieur à 1 signifie une décroissance de la population
à moyen terme.
Un taux net de reproduction s'exprime en filles par fille ou garçon
par garçon mais on peut le convertir en enfants par fille ou enfants
par garçon en utilisant le fait empirique observé que sur 205 naissances
on compte 105 garçons et 100 filles.
Age moyen à la reproduction : On distingue
l'âge moyen à la fécondité brute qui est
l'âge moyen auquel des femmes de 50 ans ont donné naissance à leurs
enfants, de l'âge moyen à la fécondité
nette qui est l'âge moyen des mères à la naissance des enfants
parmi l'ensemble des filles de la cohorte initiale (celles qui n'ont
pas eu d'enfants en particulier en raison d'un décès prématuré
comptent). Dans ce dernier cas, la mortalité durant la période féconde
est prise en compte. Il s'agit de l'âge moyen de la distribution
f(x)*l(x) et non plus de f(x) seulement.
L'âge moyen à la reproduction est un facteur important dans le calcul
de la croissance. Ainsi, on peut voir avec les paramètres pris par
défaut pour un pays africain, que la fécondité nette des hommes, soit
3,8 garçons par garçon, est largement supérieure à celle des filles
2,4 filles par fille. Néanmoins la croissance de la population stable est la même, car les femmes se
reproduisent d'un facteur moindre (2,4 filles par fille) mais plus
rapidement, tous les 27,0 ans (âge moyen à la reproduction nette),
alors que les hommes se reproduisent en plus grand nombre (3,8 garçons
par garçon) mais avec un délai plus long, tous les 41,2 ans. Le taux de
croissance qui s'en déduit est dans les deux cas égal à 3,4% par
an. Les deux points appartiennent à la même exponentielle.
Dans le cas (B) où l'épidémie de VIH existe, les femmes séropositives
contribueront également au renouvellement des générations, mais une
partie seulement (les filles non réellement porteuses du virus)
atteindront l'âge de la reproduction. Cette fraction dépend du niveau
de transmission de la mère à l'enfant qui est
fixé par défaut à 30 %.
Ainsi sur la figure figure 27, on
distingue la descendance des femmes positives au moment de la
naissance des femmes séronégatives. Dans le cas pris par défaut, c'est
à dire notamment avec une prévalence de 15 %, la descendance
nette atteint 1,85 filles par fille dont 0,26 filles nées de mères
positives, soit une croissance démographique de près de 2,5 % par
an. Ainsi, même avec un niveau de prévalence très élevé comme
15 % la croissance démographique d'un pays africain ne baisserait
que d'un pour cent.
Vous pouvez ainsi essayer d'autres niveaux de prévalence et en particulier calculer le niveau qui
correspond à un inversement de la croissance démographique. Il se
situe lorsque la prévalence dépasse 50-55 %, ce qui nous parait
aujourd'hui inconcevable. Notons que si la prévalence augmentait à des
niveaux supérieurs à 30 %, la forme de cette courbe de prévalence
selon l'âge serait vraisemblablement différente du profil retenu,
puisqu'à la fois plus importante aux âges élevés par vieillissement et
aux âges plus jeunes en raison de la forte dispersion des âges entre
partenaires en Afrique.
NB : En fait, on raisonne sur une cohorte de filles ayant atteint 15
ans et calcule sa descendance. L'ensemble des filles âgées de 15 ans
est supposée séronégative puisque qu'aucun enfant né de mère
séropositive et réellement porteur du virus n'est supposé pouvoir
survivre jusqu'à 15 ans. La fécondité des séropositives est supposée
identique à celle des séronégatives (ce qui ne sera plus vrai quand
elles pourront et désireront se faire dépister). La descendance des femmes
séronégatives est 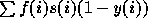 . Celles des femmes séropositives est
. Celles des femmes séropositives est 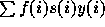 et se décompose en
fonction du niveau de la transmission de la mère à l'enfant,
et se décompose en
fonction du niveau de la transmission de la mère à l'enfant, 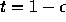 , en
, en 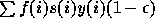 enfants qui n'atteindront pas 15 ans et
enfants qui n'atteindront pas 15 ans et 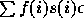 qui atteindront 15 ans et
contribueront à la reproduction de la population.
qui atteindront 15 ans et
contribueront à la reproduction de la population.
Population stable : La fécondité et la mortalité d'un
pays, si elles sont supposées invariantes dans le temps, conduisent la
population à croître ou décroître à un taux de croissance constant,
rho, dit taux de Lotka. La pyramide des âges d'une telle
population prend une forme stable quelque soit la pyramide
initiale. Dans une approche transversale, c'est à dire par exemple
lors d'un recensement, les effectifs par âge, x, décroissent
en raison de la mortalité (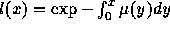 ) mais également en raison de la croissance
(
) mais également en raison de la croissance
(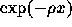 ). La proportion
d'individus âgés entre x et x+dx dans une population
stable est donc à un facteur b près
). La proportion
d'individus âgés entre x et x+dx dans une population
stable est donc à un facteur b près 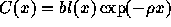 . Le rapport de la
première classe d'âge ou naissance (pour x=0), à celui de la
population totale est égale au taux brut de
natalité. b est ainsi égal au taux brut de
natalité. L'effectif de la classe d'âge x à la date
t est alors
. Le rapport de la
première classe d'âge ou naissance (pour x=0), à celui de la
population totale est égale au taux brut de
natalité. b est ainsi égal au taux brut de
natalité. L'effectif de la classe d'âge x à la date
t est alors 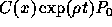 .
.
Population stable séropositive :
Il s'agit de la partie de la population stable qui est infectée.
Dans cette partie de l'ouvrage (fig 25-26-27) on fait l'hypothèse que
la prévalence du VIH parmi la population adulte et à l'état stable est
proportionnelle à un profil standard qui ressemble à celui observé
pour le VIH-1 dans certaines villes africaines, 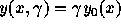 . Il y a peu de
chance que le profil de prévalence par âge soit le même pour des
hautes prévalences comme pour des basses. Quand la prévalence et la
durée de l'épidémie augmentent, l'épidémie touche proportionnellement
plus les âges élevés en raison de la longue durée d'incubation, mais
également les jeunes âges en raison de la dispersion entre les âges
des partenaires.
Il faudrait donc faire varier le profil de prévalence par âge en
fonction du niveau, ou mieux, avoir un modèle dynamique de projection.
Or, il n'est pas très aisée de construire un modèle dynamique en
particulier parce que l'épidémie concerne les deux sexes. Un tel
modèle est discuté à la fin du chapitre où on tient compte de la
dispersion des âges entre partenaires.
. Il y a peu de
chance que le profil de prévalence par âge soit le même pour des
hautes prévalences comme pour des basses. Quand la prévalence et la
durée de l'épidémie augmentent, l'épidémie touche proportionnellement
plus les âges élevés en raison de la longue durée d'incubation, mais
également les jeunes âges en raison de la dispersion entre les âges
des partenaires.
Il faudrait donc faire varier le profil de prévalence par âge en
fonction du niveau, ou mieux, avoir un modèle dynamique de projection.
Or, il n'est pas très aisée de construire un modèle dynamique en
particulier parce que l'épidémie concerne les deux sexes. Un tel
modèle est discuté à la fin du chapitre où on tient compte de la
dispersion des âges entre partenaires.
L'état stable est calculée de manière itérative. En effet, à l'état
stable, deux conditions doivent être remplies: le taux de croissance
doit résoudre l'équation de Lotka et la prévalence moyenne doit être
égale à celle prise par hypothèse. Or, pour une prévalence à l'âge
adulte donnée 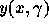 ,
on peut calculer la fontion de survie dans la cohorte (puisque la
force de mortalité à l'âge adulte est
,
on peut calculer la fontion de survie dans la cohorte (puisque la
force de mortalité à l'âge adulte est 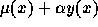 où
où  est l'inverse de la durée d'incubation), soit
est l'inverse de la durée d'incubation), soit 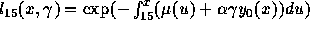 . On peut également calculer, dans une
cohorte, la proportion K de naissances dont la mère est
séropositive en notant ,
. On peut également calculer, dans une
cohorte, la proportion K de naissances dont la mère est
séropositive en notant ,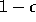 , le taux de transmisson de la mère à l'enfant:
, le taux de transmisson de la mère à l'enfant:
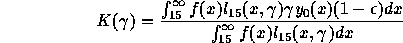
La survie dans une cohorte de nouveau-nés est la somme de deux
cohortes, l'une séronégative 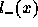 , l'autre séropositive
, l'autre séropositive
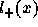 . La première ne sera affectée par le VIH qu'à l'âge adulte
et la seconde décèdera du sida avec un taux de mortalité pris égal à
1/3 par an:
. La première ne sera affectée par le VIH qu'à l'âge adulte
et la seconde décèdera du sida avec un taux de mortalité pris égal à
1/3 par an:
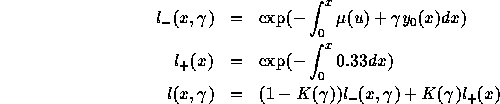
On peut alors en déduire le taux de croissance, 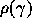 ,
par l'équation de Lotka
,
par l'équation de Lotka 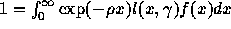 .
.
On calcule alors la nouvelle population stable (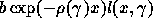 ), ce qui
permet de calculer une nouvelle prévalence moyenne parmi la population
adulte qui doit différer de la valeur voulue. On cherche par
dichotomie, la valeur de
), ce qui
permet de calculer une nouvelle prévalence moyenne parmi la population
adulte qui doit différer de la valeur voulue. On cherche par
dichotomie, la valeur de 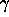 qui fournit la valeur de la prévalence moyenne
désirée.
qui fournit la valeur de la prévalence moyenne
désirée.
L'hypothèse qui consiste à conserver un profil de prévalence par
âge invariant est probablement fausse pour des hauts niveaux de
prévalence, mais pour des niveaux faibles, pour autant qu'on croit en
les rares enquêtes de prévalence, c'est acceptable.
En particulier, on peut vérifier qu'il est bien difficile de
remarquer sur la pyramide des âges la présence de l'épidémie VIH lors
d'un recensement actuel même avec une prévalence de 15 %. En
effet, avec une prévalence de 15 % la croissance démographique
reste très élevée, de l'ordre de 2 % par an, si bien que la forme
de la pyramide des âges stable est encore nettement marquée par
l'exponentielle de la croissance et non par la mortalité.
Dans le cas d'un prévalence plus élevée de l'ordre de 30 % la
croissance s'en ressent, devient plus faible, et la pyramide prend
alors la forme de la population stationnaire (ou fonction de survie),
c'est à dire très marquée aux âges adultes et aux très jeunes âges.
Taux brut de natalité : Il s'agit
simplement du rapport du nombre des naissances d'une certaine période
sur les années vécues par l'ensemble de la population sur la même
période.
Taux brut de mortalité : Il s'agit simplement
du rapport du nombre des décès d'une certaine période sur les années vécues
par l'ensemble de la population sur la même période.
Taux de croissance : Il s'agit simplement du
rapport de l'accroissement d'une population durant certaine période
sur les années vécues par l'ensemble de la population sur la même
période. Dans une population fermée, c'est à dire sans migration), il
s'agit de la différence entre le taux brut de
natalité et le taux brut de mortalité.
Prévalence du VIH.
On appelle
prévalence la proportion d'individus affectés par une maladie ou
porteurs d'un virus, en l'occurence ici le VIH. On montre dans
l'ouvrage qu'il est quasiment impossible de prévoir la
prévalence qui sévira à un horizon de 15-20 ans en Afrique en
particulier parce que l'intervalle entre deux générations d'infectés
peut être très court, de quelques mois. Dans le renouvellement d'une
population humaine, l'intervalle minimum est de 15 ans.
Dans les figures 25, 26 et 27, le niveau de prévalence est donc une
hypothèse et non un résultat.
Prévalence moyenne adulte
L'hypothèse retenue dans l'ouvrage est que la prévalence moyenne d'un
pays déjà fortement infecté aujourd'hui pourrait atteindre 15 %
parmi la population âgée de plus de 15 ans.
La prévalence varie fortement par âge et son profil se déforme au
cours du temps en raison de la longue durée
d'incubation du VIH et d'une éventuelle dérive vers les plus
jeunes en raison d'une grande dispersion des âges entre
partenaires. Néanmoins, dans l'ouvrage, comme dans cette simulation,
on retient un profil type qui s'apparente à celui observé pour le
virus HIV-1 dans certaines villes africaines en 1990.
Les valeurs de la prévalence selon l'âge sont proportionnelles à ce
profil par âge et le ratio est calculé de sorte que la prévalence
moyenne soit celle de la population stable.
Le tableau (B) donne certaines
variables calculées dans la nouvelle population stable.
On peut changer cette valeur de la prévalence par une valeur beaucoup
plus grande qu'on pourrait observer dans une grande ville africaine ou
par une valeur beaucoup plus faible, 0,4 %, qu'on observe en Ile
de France en 1990 chez les femmes enceintes.
Si on cherche à
simuler une situation occidentale avec ce modèle, il faut bien avoir
conscience qu'il s'agit d'un modèle hétérosexuel; or ce n'est pas la
situation prédominante en occident où l'épidémie est à prédominance
masculine en raison de l'homosexualité et où l'épidémie parmi les
femmes résultent essentiellement des toxicomanes. Neanmoins, si on
pouvait choisir un profil de prévalence plus réaliste pour les femmes
occidentales et admettre que la fécondité des femmes séropositives est
similaire à celles des autres femmes, ce qui n'est pas tout à fait
vrai puisque d'une part beaucoup de femmes peuvent se faire dépister
en occident, et d'autre part la situation familiale des toxicomanes
est moins stables que les autres femmes, alors le modèle serait
valable.
Le profil par âge de la prévalence du VIH-2 est très différent et
au contraire croît en fonction de l'âge, prouvant ainsi que la durée
d'incubation de ce virus est beaucoup plus longue et que l'ancienneté
de l'épidémie est également plus importante.
Le décalage entre les profils masculins et féminins reflète les
décalages d'âge entre les époux dans cette région du monde.
En raison de la transmission de la mère à
l'enfant, la prévalence n'est pas négligeable dans les tous
premiers âges de la vie. On fait néanmoins implicitement l'hypothèse
qu'aucun enfant, infecté par sa mère durant la grossesse, n'atteindra l'âge
adulte : hypothèse qui pourrait être contredite un jour.
Transmission de la mère à l'enfant: une
mère infectée par le virus HIV-1 peut transmettre le virus à son
enfant durant la grossesse, l'accouchement ou l'allaitement. Nos
connaissances sur la manière dont le virus se transmet, la phase de la
transmission et la fréquence de cette transmission s'accroissent au
fur et à mesure que les recherches progressent. L'essentiel de la
transmission aurait lieu durant l'accouchement ou en tout cas durant
les derniers mois de grossesse. L'estimation du pourcentage de
nouveau-nés infectés par leur mère durant la période néonatale a
décru avec l'amélioration de nos connaissances. En particulier
l'administration d'anti-rétroviraux durant les derniers mois de la
grossesse permettrait de limiter la transmission à moins de 10 %
selon certaines études menées dans les pays développées. Néanmoins, en
Afrique, nous avons retenu un niveau de transmission égale à
30 %. On peut faire varier ce pourcentage à des fins de
simulation. Dans les premiers modèles de simulation, c'est à dire à la
fin des années 80, on retenait un pourcentage de transmission égal à 50 %.
Durée moyenne d'incubation:
La durée d'incubation est la durée entre la primo-infection et
l'apparition des premiers symptômes du sida. La variabilité de la date
d'apparition est très grande selon les individus. L'estimation de la
moyenne de cette distribution fait l'objet de recherches importantes
notamment à partir des cohortes d'homosexuels comme celle dite de San
Francisco. On estime que la durée médiane, ou temps au bout duquel la
moitié de la cohorte a déclaré un sida et ou l'autre moitié est encore
asymptomatique, est de l'ordre de 10 ans (parmi les homosexuels des
pays développés).
La durée moyenne de survie après la déclaration de la maladie varie
selon les traitements mais reste en moyenne de l'ordre de deux ans.
En Afrique, on estime sans vraiment de données statistiques à l'appui,
que la durée médiane d'incubation serait plus courte, peut-être 8 ans.
Dans cette partie de l'ouvrage, on ne prend en compte que la durée de
survie d'un séropositif (phase asymptomatique et phase sida
regroupées) et considère pour simplifier les calculs des figures 25,
26 et 27 que ce risque est indépendant de la durée d'incubation. On
retient alors pour cette durée moyenne totale (asymptomatique + sida)
une valeur de 10 ans pour les adultes et de 2 ans pour les nouveau-nés
porteurs du virus.
Cette présentation sur le World-wide Web vous permet de changer la
valeur de la durée d'incubation. Ainsi vous pouvez entrer une durée
longue, 20 ans, qui pourrait être celle du virus HIV-2. A l'opposé,
vous pouvez entrer une valeur très courte, inférieure à l'année. Mais
dans ce dernier cas, il n'y aurait vraisemblablement pas d'épidémie,
car les personnes infectées n'auraient pas le temps de transmettre le
virus. Ainsi, notre modèle qui fixe le niveau de la prévalence est
irréaliste dans ce cas, car il ne sera jamais atteint à moins que
l'infectivité de ce virus soit beaucoup plus importante qu'elle ne
l'est pour le sida, comme par exemple pour la gonoccocie.
Pour voir rapidement l'influence de la durée d'incubation sur la
prévalence, il ne faut pas utiliser un modèle statique mais un modèle
dynamique simple sans même faire intervenir les âges.
En réalité, la durée moyenne d'incubation de VIH-1 est une des
connaissances épidémiologiques aujourd'hui les plus fiables. Si, en
raison d'un traitement efficace, cette durée d'incubation augmentait,
la prévalence serait modifiée d'une manière complexe qui dépendrait en
particulier de la nouvelle infectivité des patients prenant ce
traitement. Ici, le modèle est simple : si la durée d'incubation
est de t années et la prévalence de y %,
alors la nouvelle mortalité de la population est de tant.
- Qx Quotient de mortalité: Un quotient
de mortalité à l'âge x, Qx, est la probabilité pour
un individu d'âge x de décéder avant d'atteindre l'âge
x+1.
- lx Survie de la naissance à l'âge
x: Il s'agit de la probabilité pour un nouveau né de
survivre jusqu'à l'âge x. l(x+1)= l(x) * (1 - q(x)).
- d(x,x+1) Distribution des décès: Il
s'agit de la distribution des décès d'une cohorte de nouveaux nés,
c'est à dire du nombre des décès entre les âges x et
x+1. d(x,x+1) = l(x) - l(x+1) = l(x)*q(x).
- e(x)Espérance de vie à l'âge
x: Pour l'âge 0, il s'agit de l'espérance
mathématique de la distribution d(x,x+1), ou âge moyen au
décès d'une cohorte de nouveaux-nés. Pour un autre âge x, il
s'agit de la durée de survie au delà de l'âge x.
Orphelins: Du fait d'une mortalité
encore forte en Afrique en comparaison des autres continents, la
proportion d'orphelins est déjà, sans sida, très élevée : à 10 ans,
7 % des enfants ont perdu leur mère et 12,5 % leur père et
près de 0,8 % ont perdu leurs deux parents. Avec une prévalence
du VIH égale à 15 % prise par défaut, la proportion d'orphelins à
10 ans est multipliée par 3 environ. Il est assez difficile d'estimer
la proportion d'orphelins de père et de mère car cela est très
dépendant de la probabilité que les deux parents soient infectés
lorsque l'un l'est (20 ?) qui change drastiquement l'estimation
du nombre d'orphelins.
Informations techniques
Processus.
Il s'agit du numéro de
processus de votre simulation. Il peut vous être utile si vous faites
plusieurs simulations et avez ouvert plusieurs fenêtres. Vous pouvez
en effet soumettre une nouvelle simulation avec les menus des figures
25-26, attendre votre numéro de processus et pour, par exemple, ne pas
ouvrir une nouvelle fenêtre (ce qui peut prendre du temps) changer
uniquement le numéro de processus dans l'adresse URL de votre
fenêtre. Avec certaines visionneuses, comme Netscape, on change simplement
l'adresse de location en haut de l'écran.
L'adresse du serveur est http://sauvy.ined.fr/popafsi.
Nicolas Brouard
6 juillet 1995
Révision le 7 septembre 1995.
Nous serions heureux de recueillir vos commentaires
![[Mail]](/brd-icons/enveloppe.gif) Brouard@ined.fr
Brouard@ined.fr
Nous sommes également à la recherche de prévalence du VIH par âge afin
d'enrichir le modèle en proposant d'autres situations de par le monde.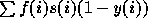 . Celles des femmes séropositives est
. Celles des femmes séropositives est 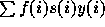 et se décompose en
fonction du niveau de la transmission de la mère à l'enfant,
et se décompose en
fonction du niveau de la transmission de la mère à l'enfant, 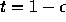 , en
, en 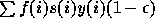 enfants qui n'atteindront pas 15 ans et
enfants qui n'atteindront pas 15 ans et 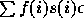 qui atteindront 15 ans et
contribueront à la reproduction de la population.
qui atteindront 15 ans et
contribueront à la reproduction de la population.
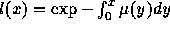 ) mais également en raison de la croissance
(
) mais également en raison de la croissance
(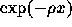 ). La proportion
d'individus âgés entre x et x+dx dans une population
stable est donc à un facteur b près
). La proportion
d'individus âgés entre x et x+dx dans une population
stable est donc à un facteur b près 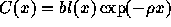 . Le rapport de la
première classe d'âge ou naissance (pour x=0), à celui de la
population totale est égale au
. Le rapport de la
première classe d'âge ou naissance (pour x=0), à celui de la
population totale est égale au 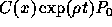 .
.
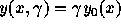 . Il y a peu de
chance que le profil de prévalence par âge soit le même pour des
hautes prévalences comme pour des basses. Quand la prévalence et la
durée de l'épidémie augmentent, l'épidémie touche proportionnellement
plus les âges élevés en raison de la longue durée d'incubation, mais
également les jeunes âges en raison de la dispersion entre les âges
des partenaires.
Il faudrait donc faire varier le profil de prévalence par âge en
fonction du niveau, ou mieux, avoir un modèle dynamique de projection.
Or, il n'est pas très aisée de construire un modèle dynamique en
particulier parce que l'épidémie concerne les deux sexes. Un tel
modèle est discuté à la fin du chapitre où on tient compte de la
dispersion des âges entre partenaires.
. Il y a peu de
chance que le profil de prévalence par âge soit le même pour des
hautes prévalences comme pour des basses. Quand la prévalence et la
durée de l'épidémie augmentent, l'épidémie touche proportionnellement
plus les âges élevés en raison de la longue durée d'incubation, mais
également les jeunes âges en raison de la dispersion entre les âges
des partenaires.
Il faudrait donc faire varier le profil de prévalence par âge en
fonction du niveau, ou mieux, avoir un modèle dynamique de projection.
Or, il n'est pas très aisée de construire un modèle dynamique en
particulier parce que l'épidémie concerne les deux sexes. Un tel
modèle est discuté à la fin du chapitre où on tient compte de la
dispersion des âges entre partenaires.
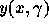 ,
on peut calculer la fontion de survie dans la cohorte (puisque la
force de mortalité à l'âge adulte est
,
on peut calculer la fontion de survie dans la cohorte (puisque la
force de mortalité à l'âge adulte est 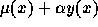 où
où  est l'inverse de la durée d'incubation), soit
est l'inverse de la durée d'incubation), soit 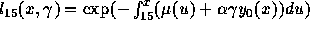 . On peut également calculer, dans une
cohorte, la proportion K de naissances dont la mère est
séropositive en notant ,
. On peut également calculer, dans une
cohorte, la proportion K de naissances dont la mère est
séropositive en notant ,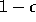 , le taux de transmisson de la mère à l'enfant:
, le taux de transmisson de la mère à l'enfant:
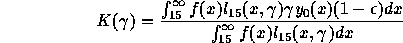
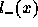 , l'autre séropositive
, l'autre séropositive
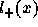 . La première ne sera affectée par le VIH qu'à l'âge adulte
et la seconde décèdera du sida avec un taux de mortalité pris égal à
1/3 par an:
. La première ne sera affectée par le VIH qu'à l'âge adulte
et la seconde décèdera du sida avec un taux de mortalité pris égal à
1/3 par an:
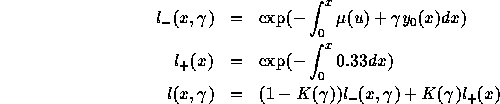
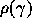 ,
par l'équation de Lotka
,
par l'équation de Lotka 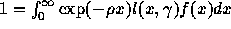 .
.
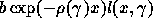 ), ce qui
permet de calculer une nouvelle prévalence moyenne parmi la population
adulte qui doit différer de la valeur voulue. On cherche par
dichotomie, la valeur de
), ce qui
permet de calculer une nouvelle prévalence moyenne parmi la population
adulte qui doit différer de la valeur voulue. On cherche par
dichotomie, la valeur de 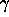 qui fournit la valeur de la prévalence moyenne
désirée.
qui fournit la valeur de la prévalence moyenne
désirée.