Life Expectancy
Enter the value of the
Life expectancy at birth before the AIDS epidemics. In the book and
by default its value is 50 years which corresponds to the global african
situation during the mid 80's.
Formally, life expectancy is the mean age at death of a cohort of
new-borns exposed to death according to mortality rates. Mortality
rates are estimated by the ratio of observed deaths between two ages
and two dates by the corresponding total time spent by the population
within the same frame limits. If the age ranges and period ranges are
not too big (typically 5 years age group and 1 year period)
demographers called them mortality rates by age group for the period
concerned. A mortality rate is expressed as the inverse of time
(typically per year), like incidence or frequency.
A more common index which can often be deduced from the mortality rate
is the probability of death between two exact ages. These
probabilities (between 0 and 1) are presented on figure 25 from page 159 in log
scale.
The size of the fictious cohort or survival function which decreased
by age is represented on figure
26. Life expectancy at birth is also the area under the survival function.
If you enter a value of 20 or 25 years instead of the 50 years
(default) you are simulating the mortality conditions which prevailed
before the demographic transition, ie before the XVIIIth century in
Europe and until the beginning of the XXth century in Africa.
If you enter 75 years you are closed to the actual situation in
developped countries.
By default the life table is computed as a Coale and Demeny model life table from the western region. Other regions
(East, North, South) are permitting other age shapes but for the same
life expectancy at birth. These small refinements are only for demographers.
It is arbitrarly assumed that the life expectancy is 2 years smaller
for males compared to females. The single parameter which can be
modified is therefore concerning life expectancy at birth for both
sexes.
Description of the AIDS epidemic impact
During the epidemic, the adult mortality will increase because adults
are primarly infected during sexual intercourse with already infected
persons. The transmission depends of many factors described in the
book. Here the new adult mortality is directly linked to the HIV
prevalence. It is assumed that the new force of mortality at age
x is equal to the previous mortality plus the prevalence rate
at that age multiplied by the inverse of the mean incubation time (it means that we are
considering that the the onset of AIDS is independent of time since
infection; this simplification is correct for that kind of results in
our point of view).
Because of the vertical transmission from
mother to child, infant mortality (before 1 year) and mortality
before 5 years will also increase.
The survival function during the epidemic is affected twice: during
infancy and during ages of sexual activity. Life expectancy, which is
also the area under the survival function is thus decreasing. Values
of the life table before and during the epidemic are obtained by
clicking on the new labels of the figures.
Model Life Tables: It has been
observed that during the mortality transition, that is during the
decline of the mortality of a country, the mortality rates are not
decreasing by the same amount at each age. Strong correlations between
age declines have been observed. In particular infant mortality is
declining at a higher speed when mortaliy is high compared to adult
mortality. A model life table is a set of survival functions for a
fictious country whose mortality will decline from 20 years of life
expectancy to 80 years or more. Thus, life expectancy is the first
most important parameter of a model life table. For a more precise
description of mortality, many authors have added a second
parameter. In the case of the Coale and Demeny model, the second
parameter is regional. Sully Ledermann (1959) observed that the infant
mortality of Italy and Spain was always higher than in other northern
countries for the same level of life expectancy. So Coale and Demeny
called them the South model and published a set of life tables with
systematic higher infant mortality and lower adult mortality. Three
other regional models like the East, North and West models were also
defined. The West model has been arbitrarly used here for Africa
without strong scientific arguments.
Model life tables are generally computed and published by 5 years
age groups, but for simulations concerning the AIDS epidemic mortality
rates by single age are required. Therefore we interpolated the
survival function using a quasi-Hermite procedure. This procedure is
not optimal and for very low mortality, unfortunate waves are visible
(only when probabilities of death are drawn in a log scale), but they do not
have influence on the simulation results.
Also results by 5 years age groups are coherent with the original
publication:
Coale, Ansley and Demeny, Paul.- Regional Model
Life Tables and Stable Population, Princeton University Press,
1966, (1983 edition, Academic Press, 496 p.
Fertility: Following a cohort, a fertility
rate at a particular age group is the ratio of the total number of
babies born from mother in the age range, divided by the total amount
of time spent by all women in the same interval of age.
Fertility curve by age of the mother are very typical for biological
reasons: starting at age of puberty (15) and stopping after age of
menopause (50). But shapes may vary according to a lot of parameters,
like age at marriage and degree of contraception use.
Fertility can also be measured according to age of fathers.
At old ages men can give birth only if the mother is in the
reproductive age. Therefore in monogamous countries, where also age of
husbands is only 2 or 3 years older than wives, male fertility does not
really differ. But in Africa, where polygamy may happen, male
fertility is still very high at age 80. Therefore, in the book we
distinguished 2 kinds of fertility regimes, european and african,
essentially because of the male fertility gap.
Fertility regime
: In the the european regime, contraception is highly used,
mostly after age 30, increasing the convexity of the fertility shape.
Male fertility will also rapidly decline for both reasons:
contraception and menopause of the wife. But in the african regime,
as age difference beetween spouses at first marriage may reach 10 years,
and as the use of contraception is very rare, male fertility
after age 50 is still very high and can stay at such a high level because
of a polygamous marriage with a younger wife.
Summing fertility rates for all reproductive ages gives the mean
number of births per woman or per man. The total (crude) fertility
does not take into account the mortality. For females it also
corresponds to the mean number of children born to women age 50 and
over. But for african males, the total fertility is not bound because
of polygamy. In our example concerning the Peul Bandé population (East
Senegal), total fertility before age 80 is about to 12 children per
man to be compared with 6.7 children per woman.
Net cumulative fertility and net reproduction
rate. Because of a high infant mortality, the size of a young
cohort of men or women will rapidly decline. Many people won't reach
the age at reproduction. The cumulative net fertility
which counts only births from survivors (f(x)*l(x)) will be
much lower than the cumulative (crude) fertility. Also for males the loss
of reproduction capacity, due to mortality is more important than for females
because male fertility is still high at older ages where survivors are
scarce.
In Africa, fertility is big enough to counterbalance the
mortality depletion. One can see on figure 27 that before the epidemic
female cohorts were already above the reproduction threshold at age 23-24
(cumulative net fertility reaches 1 at age 23-24).
The total cumulative net fertility or net reproduction rate is
2.43 at age 50 and over. A net reproduction rate lower than 1 will
correspond to a declining population.
A net reproduction rate is expressed in terms of daughters per girl or
sons per boy. It can be converted in terms of children per girl or
children per boy using the observed law that at birth there are about
105 boys for 100 girls.
Mean age at child bearing: Two kinds of
mean age at child bearing can be distinguished depending on the
inclusion or not of mortality. Crude mean age at
child bearing does not take into account mortality and
corresponds to the mean age of the distribution f(x). For women it
corresponds also to the mean age at childbearing of women surviving up to
menopause. Net mean age at child bearing
is the mean age at childbearing of an original cohort of girls. Some
of the babies will die before or during the reproductive age span,
lowering this mean age. It corresponds to the mean age of the
f(x)*l(x) distribution.
Mean age at child bearing is an important factor in the computation
of the growth rate of a population.
With the default values used in the book, the net fertility for males
is 3.8 sons per boy, which is higher than the corresponding net
fertility for females of 2.4 daughters per girl. But the induced
growth rate of the stable population is exactly the same, 3.4% per year!
Females reproduce themselves at a lower ratio (2.4) but within a shorter
period of time (27.0 years) than males who reproduce at higher ratio (3.8)
within a longer period of time (41.2 years).
In other words, both points (2.4, 27.0 and 3.8, 41.8) belong to
the same exponential curve, exp(0.034 t).
In the (B) case, that is during the epidemic, HIV positive women are
still contributing to the reproduction but only a fraction of the
babies are uninfected and will reach the age at
reproduction. Statistical estimates of the transmission rates from the mother to the baby have
been reduced during the last 5 years. The default value is 30% (click here for more details on vertical
transmission).
Therefore on figure 27 there is a
distinction between births from HIV positive women and births from HIV
negative women. In our default case with a prevalence of 15% and a
mother to child transmission rate of 30%, the total net fertility is
1.85 daughters per girl with 0.26 daughters from HIV positive
mothers. The population growth rate is 2.5% per year. Even with a high
prevalence of 15%, the growth rate will declined by 1% only.
Other HIV levels can be entered and in particular one can find the
adult HIV prevalence which makes the
population declining. The threshold corresponds to an HIV prevalence
higher that 50%. Such high prevalence levels are unconceivable in Africa
in our point of view.
If the prevalence on a national level reached more than 20 or 30%, the
age prevalence profile that we choosed in our book and simulation
wouldn't be statisfactory anymore, because the proportion of older
adults on one hand and of younger adults of the other hand would be
much more important. This comes primarly as a consequence of the high
dispersion between ages of partners in Africa which changes the age
profile of the prevalence. Long term modification of the
age profile is discussed in the book.
The key-issue to understand the reproduction of an infected population
consists in starting the reproduction process with girls aged 15 years
instead of 0. All girls age 15 years are HIV negative because no
infected baby is supposed to survive until age 15 (with our actual
knowledge so far).
Fertility of HIV positive women is supposed to be identical to HIV
negative women fertility (this is another important unknown
assumption). The net cumulative fertility is then equal to 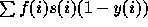 for HIV-
women. HIV+ women fertility,
for HIV-
women. HIV+ women fertility, 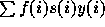 , can be decomposed, according to the
transmission rate from mother to child,
, can be decomposed, according to the
transmission rate from mother to child, 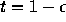 , into
, into 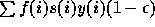 infected children who won't
reach age 15 and
infected children who won't
reach age 15 and 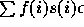 non infected children who will contribute to the
reproduction.
non infected children who will contribute to the
reproduction.
Stable population :
If fertility and mortality rates are constant in time, the population
tends to increase (or decrease if the net reproduction rate is lower
than 1) at a constant rate, called the Lotka's growth rate. Also the age
pyramid tends to a stable age profile, independent of the original
profile.
In the longitudinal approach, the size of a cohort is decreasing at
each age according to the mortality rate. But as each initial cohort
is of different size according to the growth rate of the population,
in a cross-sectional approach, profile at age x is decreasing
according to both terms: 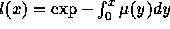 because of mortality and
because of mortality and 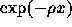 because of the
population growth ($\rho$).
because of the
population growth ($\rho$).
Equation of the proportion of the population aged between x
and x+dx is then 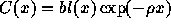 . Ratio of the first age class
(x=0) or births to the total population is therefore the crude birth rate (thus defining b). Real size
of the population at time t and age x is
. Ratio of the first age class
(x=0) or births to the total population is therefore the crude birth rate (thus defining b). Real size
of the population at time t and age x is 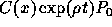 .
.
HIV positive stable
population
We are defining it as the part of the
population which is HIV positive at the stable.
The basic hypothesis in this part of the book (fig 25-26-27) is to
assume that the age profile of the HIV prevalence is proportionate to
a constant age profile which is likely to be found in actual african
cities for HIV-1, 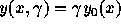 . In fact, prevalence by age will change according to
its level and past history of the epidemic, getting older because of
the long incubation time and younger because of the high dispersion of
ages between partners. At the end of chapter 3, you will find a
discussion on long term prevalence levels according to various
dispersion of age between partners and rates of partners change.
. In fact, prevalence by age will change according to
its level and past history of the epidemic, getting older because of
the long incubation time and younger because of the high dispersion of
ages between partners. At the end of chapter 3, you will find a
discussion on long term prevalence levels according to various
dispersion of age between partners and rates of partners change.
The stable state is computed iteratively. In fact, at the stable
state, two conditions have to be satisfied: the growth rate should
satisfy the Lotka's equation and the mean prevalence in the final
stable population should be equal to the requested value.
For a given prevalence 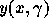 the force of mortality is
the force of mortality is
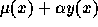 for adults, where
for adults, where  is the
inverse of the mean incubation time. Therefore, the survival function
is:
is the
inverse of the mean incubation time. Therefore, the survival function
is: 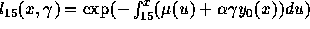 .
.
In a cohort of women, the proportion K of HIV infected
babies is, if we denote 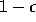 the vertical transmission from mother to child:
the vertical transmission from mother to child:
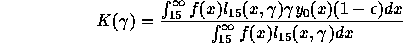
The survival function in a cohort of new borns is the sum of survival
function corresponding to 2 cohorts, one being HIV negative at
birth,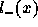 , the other
being the infected children,
, the other
being the infected children, 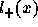 . The former will eventually be infected at adult
ages only. The latter will die from AIDS (it is assumed here that the
mean survival duration is 2 or 3 years, in fact it is not really known).
. The former will eventually be infected at adult
ages only. The latter will die from AIDS (it is assumed here that the
mean survival duration is 2 or 3 years, in fact it is not really known).
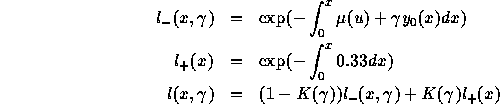
The growth rate can be deduced 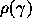 from Lotka's equation
from Lotka's equation 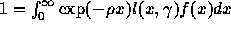 .
.
The new stable population is then computed as 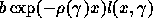 . This
leads to a new prevalence of the population aged 15 and higher, which
differs from the requested value. The correct value of
. This
leads to a new prevalence of the population aged 15 and higher, which
differs from the requested value. The correct value of 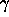 is
reached by dichotomy.
is
reached by dichotomy.
The hypothesis which consists in assuming that the age prevalence
profile is constant is probably bad for high prevalence. But for low
prevalence as far as we believed in the quality of the rare prevalence
surveys, it can be acceptable.
In particular it can be verified, that an AIDS epidemic would be very
difficult to discover from a population census! The age pyramid is
only slightly affected: even if the adult prevalence reaches 15%, the growth
rate is still very high, the (cross-sectional) age pyramid is rather
affected by the exponential growth, and the influence of mortality is small.
In the case of a much higher prevalence level, about 30%, then the
growth rate is low, and the age pyramid will be highly affected by the
mortality, modifying the dependency ratio, increasing adult depletion
and infant mortality.
Crude birth rate:
The crude birth rate is simply the number of births occuring during a
short period of time divided by the person-years lived by the total
population during the same period of time.
Crude mortality rate:
The crude mortality rate is simply the number of deaths occuring during a
short period of time divided by the person-years lived by the total
population during the same period of time.
Growth rate :
The growth rate of a population is the population increment (or
decrement) during a period of time divided by the person-years lived
by the total population during the same period of time.
In a closed population, it corresponds to the difference between the
crude birth rate and the crude mortality rate.
HIV prevalence.
The prevalence of a disease is the proportion of people infected by
the disease.
In the case of the AIDS epidemic, we proved in the book that it
is very difficult to forecast the epidemic over 15 or 20 years,
because of the very short minimal interval of time between two
generations of infected (date of infection of the secondary case minus
date of infection of the primary case) which could be a single
month. In the renewal of human population, this minimum interval which is
the age at puberty is much higher.
Remark: In figures 25, 26 and 27, the prevalence level is an hypothesis and
not an output.
Mean adult prevalence
In our book, our worst prediction for an already highly infected
population at the national level of a african country is a mean adult
prevalence of 15%. Adult population here is the sexually active population
or population aged 15 and above.
HIV prevalence varies according to age and the profile changes over
time: getting older because of the long incubation time but eventually younger too because of a
high dispersion of ages between partners in Africa.
Nevertheless, in our book we retained an age profile which is close
to the actual situation for HIV-1 in some african cities in 1990.
Age specific prevalence values are proportionate to this age profile
and the factor of proportionality is computed such that the mean adult
prevalence in the final stable population
correspond to the input value.
Table (B) gives some of the variables
computed at the stable state.
One can change the prevalence level either which a much higher value,
simulating the possible actual situation in some African cities or with
a much lower value, like 0.4%, which is the actual (1990) situation in the
region Ile de France (around Paris) among pregnant women.
But if want to simulate some western situations, we have to remember
that our model is an heterosexual model, that is where both men and
women are infected in about the same proportions. And in Western
countries, the Aids epidemic is predominantly a male epidemic because of
male homosexuality. Also the female epidemic is predominantly among
intravenous drug users. But if we could input a realistic prevalence
age profile for women in Western countries, and if we could assumed
that the fertility of drug users did not differ from other women, then
the long term situation of the epidemic and its demographic
consequences could be approached with our model.
HIV-2 age profile is very different from HIV-1 profile as it is
increasing slowly with age. Thus this is a proof that the mean
incubation time for HIV-2 is much longer than for HIV-1. Also HIV-2
epidemic seems to have reached an endemic state since decades and even
is declining in Abidjan for example.
The gap between male and female age prevalence profiles reflects the age
difference which often occurs in African countries.
Because of the high transmission probability of the
virus of the mother to its child, prevalence at very young ages is
not neglectable. It is assumed here that an infected child wouldn't reach
the adult age. This hypothesis might be wrong in the future.
Mother to child transmission :
An HIV-1 infected mother can transmit the virus to her baby, during the
pregnancy, during the delivery and during breast feeding.
Our knowledge on the transmission is more and more important as
research results are published.
The transmission seems mostly to occur during delivery and also during
the last months of pregnancy. The estimate and also the real perinatal
transmission rate has decreased as our knowledge has increased. In
particular, injection of AZT during pregnancy or even during the last
6 months of pregnancy give substantial reduction of the transmission in
an European collaborative study, reducing the rate to less than 10%.
Nevertheless in Africa the actual guess is about 30% of transmission.
Mean incubation time:
The incubation time is the time between infection and the onset of
AIDS. This duration varies according to individuals. Estimates of the
distribution has been and is an important research subject. Most
important data come from homosexuals cohort studies, like the San
Francisco cohort study. From these data, the median time or time where
half of the original cohort is still asymptomatic, is about 10 years.
The survival time after the onset of AIDS varies according to people
and treatments but is estimated to about 2 years.
In Africa, but without strong scientific data, it is estimated that
the mean incubation time is smaller, about 8 years.
In this part of our book, asymptomatic and
symptomatic phases are added. Also, for the computation of figures
25, 26 and 27, we are simplifying the reality by assuming that the
risk of dying from AIDS is independent of the time since infection. If
the mean incubation for adults is about 10 years then the supplemental
risk of an infected adult is 0.1 per year. Incubation and survival
time for new borns is much shorter. The default value is 2 years but
some new litterature are mentioning longer survival times.
The world-wide web presentation lets you change this mean
incubation. So you can try a very long incubation time like 20 years
which could be the value for HIV-2. On the other hand, you can chose a
very short mean incubation time, lower than a year. But in that case,
an epidemic would probably not appear, because infected people would
not have time to transmit the virus. In that case our model, which
fixes the HIV prevalence level, is unrealistic because such a level
would not probably be reached unless the infectivity of this virus is
much higher than HIV, like gonorrhea for example! In such a case we
should change the acceptable prevalence level or, better, let the
prevalence level be endogeneous in the model.
To rapidly perceive the influence of incubation time on the level of
prevalence, we won't use a static model but a simpler dynamic model
without age.
Incubation time is in fact one the best estimated parameter for
HIV-1. When treatments will be efficient, incubation time will be
longer and it is not clear if it will increase the prevalence level
while it mostly depends on the infectivity period. Our model is not
involved in such kind of research. We are only saying that if at
equilibrium the HIV prevalence reaches the requested input level, then
we are able to compute the new demographical dynamic of the total
population.
Qx Probability of death: It is the
probability at age x to die before reaching age
x+1
lx Survival function:
It is the cumulative probability for a baby to reach age x.
l(x+1)= l(x) * (1 - q(x)).
d(x,x+1) Distribution of death:
It is the distribution density of age at death of a cohort of new-born or the
probability for a new born to die within the age range x and
x+1. d(x,x+1) = l(x) - l(x+1) = l(x)*q(x).
e(x)Life expectancy at age
x: At age 0, it is the mathematical expectancy of the
distribution of age at death d(x,x+1) or the mean duration of
life. At a another age it is the remaining mean duration of life.
Orphans:
As mortality is still very high in Africa compared to other
continents, proportion of orphans is very high even without AIDS: 7%
of children aged 10 have already lost their mother and 12.5% their
father and about 0.8% lost both parents. With a prevalence of HIV
amongst adults of 15%, proportion of orphan are multiplied by 3.
NB. It is not so easy to estimate the proportion of orphans of both
parents because it depends of the relatively unknown probability
of transmission within a partnership (20%?) which has a dramatic effect of
the number of orphans.
Some technical informations
Process Identification.
It is the number of the process related to your simulation. It can
help you to save time if you are making numerous simulations with
already open windows or clones. In that case you can update your window
by changing the id directly in the address location. On some nice
browsers, like Netscape, this
can be done directly on the address location at the top of your
window.
Temporary files (html and images) are kept, according to the
traffic on the server, between half an hour and a hour.
The address of this server is http://sauvy.ined.fr/popafsi/english.
Nicolas Brouard
26 August 1995.
Revised 19 April 1996.
Please send any comments
![[Mail]](/brd-icons/enveloppe.gif) Brouard@sauvy.ined.fr
Brouard@sauvy.ined.fr
We are looking for real HIV prevalence rates observed in the World to
improve our simulation and to open it to the Asian situation, in
particular.
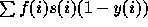 for HIV-
women. HIV+ women fertility,
for HIV-
women. HIV+ women fertility, 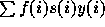 , can be decomposed, according to the
transmission rate from mother to child,
, can be decomposed, according to the
transmission rate from mother to child, 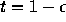 , into
, into 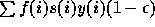 infected children who won't
reach age 15 and
infected children who won't
reach age 15 and 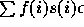 non infected children who will contribute to the
reproduction.
non infected children who will contribute to the
reproduction. 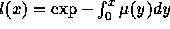 because of mortality and
because of mortality and 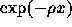 because of the
population growth ($\rho$).
because of the
population growth ($\rho$). 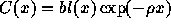 . Ratio of the first age class
(x=0) or births to the total population is therefore the
. Ratio of the first age class
(x=0) or births to the total population is therefore the 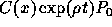 .
.
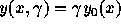 . In fact, prevalence by age will change according to
its level and past history of the epidemic, getting older because of
the long incubation time and younger because of the high dispersion of
ages between partners. At the end of chapter 3, you will find a
discussion on long term prevalence levels according to various
dispersion of age between partners and rates of partners change.
. In fact, prevalence by age will change according to
its level and past history of the epidemic, getting older because of
the long incubation time and younger because of the high dispersion of
ages between partners. At the end of chapter 3, you will find a
discussion on long term prevalence levels according to various
dispersion of age between partners and rates of partners change.
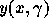 the force of mortality is
the force of mortality is
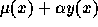 for adults, where
for adults, where  is the
inverse of the mean incubation time. Therefore, the survival function
is:
is the
inverse of the mean incubation time. Therefore, the survival function
is: 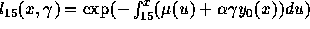 .
.
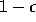 the vertical transmission from mother to child:
the vertical transmission from mother to child:
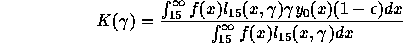
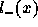 , the other
being the infected children,
, the other
being the infected children, 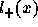 . The former will eventually be infected at adult
ages only. The latter will die from AIDS (it is assumed here that the
mean survival duration is 2 or 3 years, in fact it is not really known).
. The former will eventually be infected at adult
ages only. The latter will die from AIDS (it is assumed here that the
mean survival duration is 2 or 3 years, in fact it is not really known).
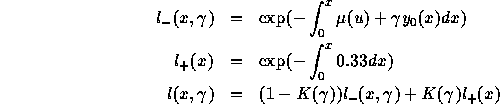
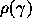 from Lotka's equation
from Lotka's equation 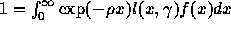 .
.
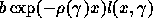 . This
leads to a new prevalence of the population aged 15 and higher, which
differs from the requested value. The correct value of
. This
leads to a new prevalence of the population aged 15 and higher, which
differs from the requested value. The correct value of 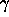 is
reached by dichotomy.
is
reached by dichotomy.