Mathematical Demography Exam

DESS IDP Paris I (N. Brouard)

14 juin 1995, 3 hours, without document

The original exam did consist in two exercises and a problem. Only the problem has been translated until now.

Questions are in italics and proposed solution in roman. This exam can be found on the WEB/Internet : http://sauvy.ined.fr/ brouard/enseignement

Problem: Force of mortality at very old ages

We are interested in analyzing mortality at very old ages and particularly on the shape of the mortality force beyond age 90. Let us take the example of a woman who is supposed to be 120. We will take into account the possibility of identity swap between mother and daughter.

The daughter is supposed to be exactly 20 years younger than her mother and to have died at age 40. To simplify we use a recent period life table which is far from the 1874 cohort life table but similar at high ages.

1. Logarithmes of mortality rates of a period life table are well adjusted by the Gompertz line from age 40 to age 90. Before age 90, forces and central rates are very similar, hence the confusion the two. Beyond age 90, mortality rates are difficult to estimate mainly because the sample sizes are too small but also because the force of mortality, about 0.2 per year, is too high for the time unit. Consequently results provided by the usual methods of computing the rates differ. Estimating the force of mortality at old ages and testing the Gompertz hypothesis is a challenge for research.

   Mortality rate (or force) at age 40, , is about 2.28 per thousand per year and is about 75.39 per thousand per year at age 80. Give the expression of the force of the Gompertz law at age x:

   

   

   and

   

2. What is the level reached by the force of mortality if the Gompertz law still holds until age 120?

   

3. Let sg(x) the conditional probability to survive for age 40 to age x in the case of the Gompertz law. Give the expression of sg(x) in respect to a, b, and .

   

4. Verify that sg(90)/sg(40) is about 13%.

   

   

5. Compute the conditional probability for a person aged 90 to survive until age 100, 110 and 120 in the case of the Gompertz assumption.

   

   

   

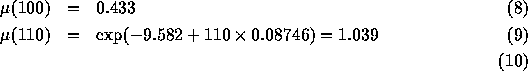
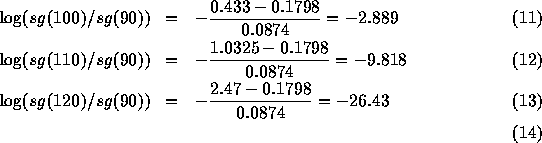
   from which:

   

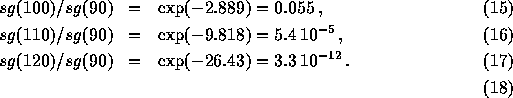
   Assuming that 6 billion humans are alive at age 90, how many will reach age 120 using the Gompertz assumption?

   What can you infer from these results about the possibility for a country like France (population: 58 million) to have a senior citizen aged 120?

   If six billion people are aged 90, only =0,0198 individual(s) could survive until age 120! The standard deviation of this binomial law , = 0,27 is also very small proving that there cannot be any human survivor.

6. On the opposite, let us now suppose that the force of mortality is flat after age 90, ie mortality still exists but without any aging, and equal to the level found at age 90. Give the expression of the conditional probability to survive from age 90 until age x.

   In the case where force of mortality is constant, the survival function, sc, is a decreasing exponential:

   

   Answer the previous questions with the hypothesis of a constant force instead of a Gompertz law.

   

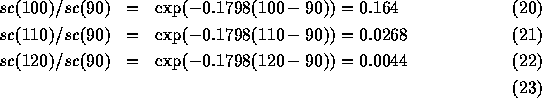
   From the 6 billion people, millions would now have reached age 120!

7. Assuming the Gompertz law, compute the probability for a woman, aged 60 when her 40 year old daughter died, to reach age 120.

   Result is straight forward:

   

8. If the daughter takes the identity of her mother at the death of the latter, what is the probability for the former to reach age 120-20=100.

   Probability is easily derived:

   

   The probability of living 60 more years differs if you are 40 or 60 years old. How significant is this difference in the case of the Gompertz assumption? Is this a proof of mistaken identity?

   The probability for the 40 year old daughter to reach age 100 is 7 per thousand whereas there is no chance for the 60 year old mother to have reach age 120.

   If the Gompertz law still holds after age 90, the mistaken hypothesis is validated: there was an identity swap.

     
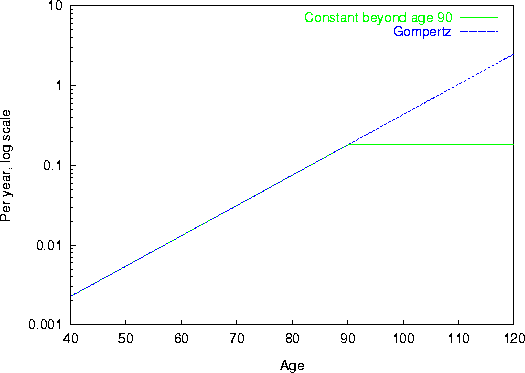
   Figure 1: Hypotheses concerning mortality forces beyond age 90: constant or Gompertz.
   

9. Compute the above mentioned difference using the hypothesis of a constant force of mortality after age 90. What can you conclude?

   The computation of the new probabilities follows:

   

   and

     
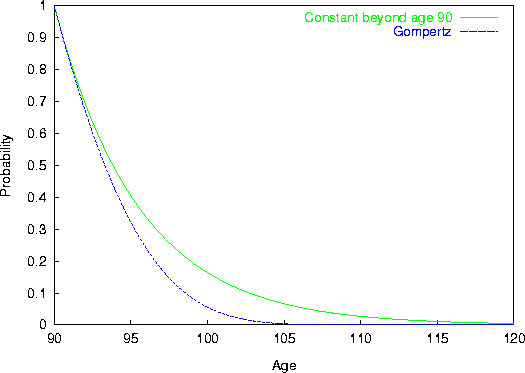
   Figure 2: Conditional probability of surviving for a human aged 90 according to two hypotheses: constant mortality force or extension of a Gompertz line.
   

   

   Figures 1 and 2 summarize the hypotheses on the mortality force and on its consequences on the survival curves.

   In the case of a constant mortality force beyond age 90, the probability for the mother to survive until age 120 is only 7 times lower than the probability of the daughter to reach age 100.

   Research at high ages and in particular on centenarians is necessary to have better estimates on mortality at age hundred and above. Nevertheless, if the force of mortality at very old age was plateauing among humans, like it seems to be verified for insects like drosophila we should find many 120 year olds in China!