L'estimation de la force de mortalité aux grands âges et la remise en cause de la loi de Gompertz sont des questions ouvertes auprès des chercheurs.
Le taux ![]() vaut 2,28 pour mille par an et celui à 80 ans
vaut 75,39 pour mille et par an. Donner l'expression numérique de
la force de mortalité de la loi de Gompertz pour tous les âges
supérieurs à 40 ans :
vaut 2,28 pour mille par an et celui à 80 ans
vaut 75,39 pour mille et par an. Donner l'expression numérique de
la force de mortalité de la loi de Gompertz pour tous les âges
supérieurs à 40 ans :
![]()
La réponse est immédiate :
![]()
et
![]()
![]()
![]()
![]()
![]()
![]()
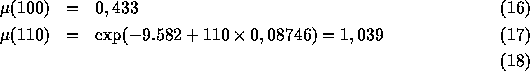
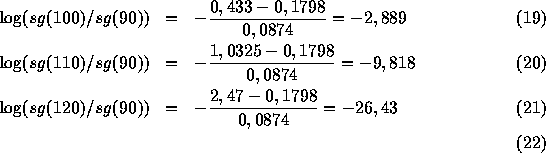
d'où :

Si 6 milliards d'individus survivaient jusqu'à 90 ans, combien atteindraient-ils 120 ans? Qu'en déduisez vous sur la possibilité pour un pays comme la France d'avoir une personne âgée de 120 ans?
Si 6 milliards d'individus survivaient jusqu'à 90 ans, ![]() =0,0198 individus, soit même pas un
individu ne survivrait jusqu'à 120 ans. L'écart type de cette loi
binomiale,
=0,0198 individus, soit même pas un
individu ne survivrait jusqu'à 120 ans. L'écart type de cette loi
binomiale, ![]() = 0,27, serait également très faible, il n'y
aurait donc aucun survivant.
= 0,27, serait également très faible, il n'y
aurait donc aucun survivant.
Dans le cas où la force de mortalité est indépendante de l'âge, la fonction de survie est une exponentielle décroissante :
![]()
Répondez aux diverses sous-questions de la question précédente dans le cas d'une force de mortalité constante au delà de 90 ans.

Sur 6 milliards, il y aurait ainsi ![]() millions de survivants à 120 ans !
millions de survivants à 120 ans !
![]()
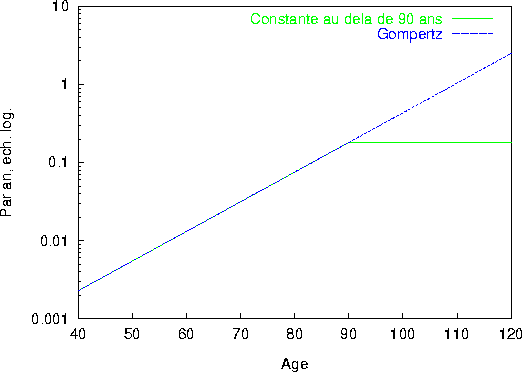
Figure: Hypothèses sur les forces de mortalité au delà de 90
ans : constante ou Gompertz.
La probabilité se calcule aisément :
![]()
Il y a-t-il une grande différence entre ses deux probabilités de survivre durant 60 ans ? Si on admet la loi de Gompertz, ces résultats sont-ils pour vous la preuve statistique d'une usurpation d'identité ?
Il y a donc 7 chances sur mille pour une fille de 40 ans d'atteindre 100 ans et aucune chance pour la mère de 60 ans d'atteindre 120 ans. Si la loi de Gompertz est vérifiée, il y a usurpation d'identité.
![]()
et
![]()
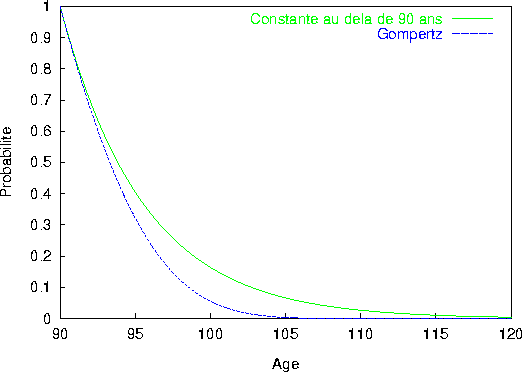
Figure 2: Fonctions de survie au delà de 90 ans selon l'hypothèse
d'une constance de la mortalité au delà de 90 ans ou d'une
prolongation de la droite de Gompertz.
retracent les hypothèses sur la force de mortalité et ses conséquences sur les fonctions de survie.
Dans le cas d'une force de mortalité constante au delà de 90 ans, l'usurpation d'identité n'est pas prouvée puisque la probabilité pour la mère de survivre jusqu'à 120 ans n'est que 7 fois moindre que celle pour la fille de survivre jusqu'à 100 ans.
Il faut donc faire des recherches, en particulier sur les centenaires, pour mieux estimer la mortalité à 100 ans. Si la force de mortalité s'infléchissait aux âges très élevés comme cela semble être prouvé pour certains insectes comme les drosophiles, on devrait néanmoins trouver beaucoup de personnes âgées de 120 ans en Chine !